
Un diagrama de dispersión, también conocido como gráfico de dispersión o scatter plot en inglés, es una herramienta gráfica utilizada para observar y analizar la relación entre dos variables. Este tipo de gráfico representa los datos como un conjunto de puntos en un plano cartesiano, donde cada punto corresponde a los valores de dos variables.
Es especialmente útil en estudios estadísticos y en análisis de correlación, permitiendo identificar patrones, tendencias y posibles anomalías en la información. Además, su simplicidad y claridad hacen que sea una opción accesible incluso para aquellos que no cuentan con una formación técnica en estadística.

Entendiendo el diagrama de dispersión
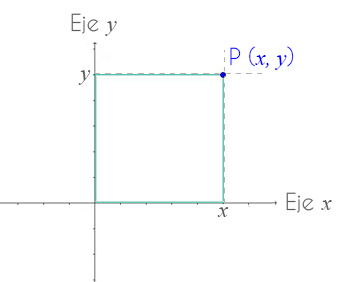
Un gráfico de dispersión es un gráfico que muestra la relación entre dos variables continuas. En este gráfico, cada punto en el plano cartesiano representa un par de valores correspondientes a una observación individual de las dos variables en cuestión.
Por ejemplo, si estamos analizando la relación entre la altura y el peso de un grupo de personas, cada punto en el diagrama representaría la altura y el peso de cada individuo. Al observar cómo se distribuyen los puntos, podemos identificar si existe una relación positiva, negativa o nula entre las variables. Esta visualización facilita la detección de patrones y tendencias, así como la identificación de posibles valores atípicos.
Objetivos del diagrama de dispersión
Estos gráficos de dispersión tienen varios objetivos clave en el análisis de datos que pueden ayudarte a comprender mejor. Algunos de estos objetivos incluyen:
Uno de los objetivos principales es identificar relaciones entre dos variables específicas. Otro objetivo es que permiten identificar y analizar patrones generales en grandes conjuntos de f. Esto incluye la identificación de tendencias lineales, como un aumento constante en el valor de una variable a lo largo del tiempo, así como tendencias no lineales, donde los cambios pueden seguir una curva en lugar de una línea recta.
Otro de los objetivos de este tipo de gráficos es que ayuda a observar cómo se distribuyen los datos alrededor de una línea de tendencia, proporcionando información sobre su variabilidad. Finalmente, se puede mencionar que proporcionan una representación visual clara y accesible de la información, permitiendo una interpretación sencilla incluso para personas sin formación técnica en estadística.
Estos objetivos hacen del diagrama de dispersión una herramienta esencial en la exploración y análisis de datos, permitiendo una comprensión más profunda de las relaciones y patrones subyacentes.
La correlación en diagramas de dispersión
La correlación es una medida estadística de la relación entre dos variables. Para el caso de este artículo, a correlación se puede observar visualmente a través del patrón que forman los puntos. Si los puntos tienden a agruparse en una forma lineal o curva, esto indica una relación positiva entre las variables. Por otro lado, si los puntos se distribuyen sin seguir ningún patrón claro, entonces indican una correlación nula o negativa.
Es importante tener en cuenta que un diagrama de dispersión solo muestra la relación entre dos variables y no necesariamente implica una relación causal. Es decir, una correlación positiva entre dos variables no significa necesariamente que una causa la otra.
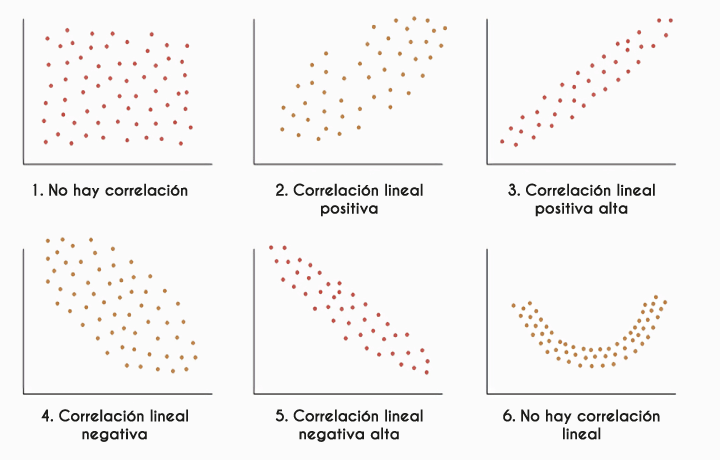
La correlación positiva
Ésta se manifiesta cuando los puntos exhiben una tendencia ascendente al moverse de izquierda a derecha en el gráfico. Esto significa que, a medida que los valores de una variable aumentan, los valores de la otra variable también tienden a incrementar. Esta relación indica una conexión directa entre las dos variables, sugiriendo que un cambio en una generalmente está asociado con un cambio similar en la otra.
Este tipo de relación es útil para identificar factores que influyen mutuamente y puede servir de base para tomar decisiones informadas en procesos de mejora continua o estrategias de optimización.

La correlación negativa
En este caso se identifica cuando los puntos muestran una tendencia descendente al moverse de izquierda a derecha en el gráfico. Esto significa que, a medida que una variable aumenta, los valores de la otra variable tienden a disminuir. La correlación negativa refleja una relación inversa entre las dos variables, indicando que un aumento en una variable está asociado con una disminución en la otra.
Por ejemplo, consideremos que un gráfico de dispersión que representa la relación entre la cantidad de ejercicio realizado y el nivel de estrés percibido. Si los puntos en el gráfico muestran que a mayor tiempo dedicado al ejercicio corresponden menores niveles de estrés, entonces existe una correlación negativa entre el tiempo de ejercicio y el estrés percibido.
La correlación nula
Una correlación nula se caracteriza por la ausencia de cualquier patrón evidente en la distribución de los puntos . En otras palabras, los puntos se encuentran dispersos al azar sin mostrar ninguna tendencia ascendente ni descendente. Esto indica que no existe una relación lineal significativa entre las dos variables analizadas.
Comprender una correlación nula es importante porque ayuda a evitar falsas conclusiones sobre posibles relaciones entre variables. Al identificar que dos variables no tienen una relación significativa, los analistas y los investigadores pueden enfocar sus esfuerzos en otras áreas que sí posean alguna interdependencia significativa, optimizando así el tiempo y los recursos invertidos en el análisis de datos.
Correlación curvilínea
Ésta se observa cuando los puntos de datos forman un patrón que sigue una curva en lugar de una línea recta. Este tipo de correlación indica una relación no lineal entre las dos variables, lo que sugiere que los cambios en una variable no se corresponden de manera constante con los cambios en la otra.
Creación de un diagrama de dispersión
Crear un diagrama de dispersión implica varios pasos básicos que aseguraran que el gráfico sea claro y útil para el análisis. A continuación se describen los pasos esenciales para la elaboración de un diagrama de dispersión:
1. Recolección de datos
El primer paso es recolectar los datos correspondientes a las dos variables que se desean analizar. Es crucial que la información sea precisa y representativa para obtener un análisis significativo. La información puede ser extraída de encuestas, bases de datos, experimentos u otras fuentes fiables.
2. Organización
Una vez recolectada, la información debe ser organizada en un formato que facilite su análisis, como una hoja de cálculo. Usualmente, se coloca una variable en la columna A (variable independiente) y la otra en la columna B (variable dependiente).
3. Creación del gráfico
Primero, organiza los datos en las respectivas columnas. Luego, dibuja un diagrama de dispersión trazando cada punto en función de sus coordenadas en los ejes X e Y.
Cómo hacerlo en Excel
Crear un diagrama de dispersión en Excel es un proceso sencillo y directo que puede resultar muy útil para visualizar la relación entre dos variables. A continuación, se detallan los pasos para generar un diagrama de dispersión en Excel:
Paso 1: Abre Excel y carga los datos. Abre Excel en tu ordenador y carga los datos que deseas analizar. Asegúrate de que la información esté organizada de manera que una variable esté en una columna (por ejemplo, la columna A) y la otra variable en la columna adyacente (por ejemplo, la columna B).
Paso 2: Selecciona los datos. Elige las celdas que contienen los datos de ambas columnas. Puedes hacerlo haciendo clic y arrastrando el cursor sobre las celdas relevantes o seleccionando la primera celda y usando las teclas Shift y flecha para seleccionar el rango.
Paso 3: Insertar el diagrama de dispersión. Con la selección realizada, ve a la pestaña “Insertar” en la barra de herramientas de Excel. Busca el grupo de gráficos y haz clic en el ícono de “Diagrama de dispersión” o “Scatter”. Aparecerá un menú desplegable con varias opciones de diagramas de dispersión. Selecciona el estilo de diagrama de dispersión simple para empezar.

Paso 4: Personalizar el diagrama. Una vez que el diagrama se ha insertado en la hoja de cálculo, puedes personalizarlo para mejorar su claridad y presentación. Añade títulos a los ejes, modifica el título del gráfico, cambia los colores y los marcadores de los puntos de datos, entre otras opciones. Para ello, haz clic en el gráfico y utiliza las opciones disponibles en las pestañas de “Diseño” y “Formato”.
Paso 5: Interpretar y analizar. Con el diagrama de dispersión listo, puedes analizar los patrones visibles en los puntos de datos. Busca tendencias, correlaciones (positivas, negativas o nulas), y cualquier otra característica destacada que pueda ayudarte en tu análisis de las variables.
Crear un gráfico de dispersión en Excel permite explorar visualmente la relación entre dos variables de manera rápida y efectiva, facilitando la toma de decisiones informadas basadas en datos.
5. Etiquetado y personalización
Después de crear el gráfico, es importante etiquetar correctamente los ejes del gráfico con los nombres de las variables correspondientes. Además, personalizar aspectos como el título del diagrama, el tamaño de los puntos y el color puede ayudar a mejorar la claridad y el impacto visual de tu presentación.
6. Análisis e interpretación
Finalmente, analiza el patrón de dispersión de los puntos en el gráfico para identificar si hay alguna correlación entre las variables. La observación de tendencias como una línea ascendente o descendente, curva, o dispersión aleatoria ayudará a determinar el tipo de relación existente.
Cómo trazar los puntos de datos
Los puntos de datos se trazan en dos ejes, generalmente el eje x y el eje y. El eje x representa una de las variables y el eje y representa la otra variable. La decisión sobre qué variable se debe colocar en el eje x y cuál en el eje y depende de la naturaleza de las variables y del propósito del análisis. Generalmente, la variable independiente se coloca en el eje x, mientras que la variable dependiente se coloca en el eje y.
Variable independiente
La variable independiente es aquella que se presume que influye o causa cambios en la otra variable. Por ejemplo, si se está analizando la relación entre el tiempo de estudio (horas) y el rendimiento académico (calificaciones), el tiempo de estudio sería la variable independiente.
Variable dependiente
La variable dependiente, por otro lado, es la que se espera que se vea afectada por la variable independiente. En el mismo ejemplo, el rendimiento académico sería la variable dependiente, ya que puede variar según las horas de estudio.
Casos especiales
En algunos casos, la relación entre las variables puede no ser claramente una de causa y efecto. En tales situaciones, la elección del eje puede basarse en la convención del campo de estudio, o en consideraciones prácticas de la presentación del gráfico. Por ejemplo, en un análisis de correlación entre altura y peso, ninguna de las variables se considera típicamente como dependiente de la otra, por lo que cualquiera podría ir en el eje x o y.
Determinar correctamente las variables para los ejes del diagrama de dispersión es crucial para una representación precisa y comprensible de los datos.
Ventajas y posibles limitaciones
Crear y utilizar un gráfico de dispersión ofrece varias ventajas importantes:
- Claridad visual: Permite observar de manera inmediata y visual cualquier relación o patrón entre dos variables.
- Identificación de tendencias: Facilita la detección de tendencias, como líneas ascendentes o descendentes, curvas, o dispersión aleatoria, que pueden orientar la toma de decisiones.
- Practicidad: Es una herramienta útil y accesible, que puede ser utilizada en una variedad de programas y aplicaciones, como Excel, para analizar datos de manera eficiente.
- Comparación visual: Facilita la comparación entre diferentes conjuntos de datos y variables, proporcionando una manera sencilla de interpretar complejas informaciones.
Limitaciones
Aunque los gráficos de dispersión son herramientas poderosas, también tienen ciertas limitaciones:
- Datos bidimensionales: Solo pueden mostrar la relación entre dos variables a la vez, lo que puede no ser suficiente para análisis más complejos que involucren múltiples variables.
- Correlación vs. causalidad: Pueden mostrar correlaciones entre variables, pero no necesariamente indican causalidad. Es importante no concluir que una variable causa cambios en otra sin un análisis adicional.
- Sensibilidad a datos atípicos: Los puntos de información atípica pueden distorsionar las interpretaciones visuales del gráfico, afectando la percepción de la relación entre variables.
- Simplicidad excesiva: En algunos casos, la simplicidad del diagrama de dispersión puede ocultar detalles importantes y matices del comportamiento de los datos.
Teniendo en cuenta estas ventajas y limitaciones, es importante utilizar los diagramas de dispersión como parte de un análisis más amplio y considerado.
Consejos para gráficos de dispersión efectivos
Para aprovechar al máximo los diagramas de dispersión y asegurar una representación clara y precisa de los datos, ten en cuenta los siguientes consejos:
- Selecciona adecuadamente las variables: Asegúrate de que las variables seleccionadas tengan una relación teórica o sustantiva que sea de interés. Esto aumenta la probabilidad de obtener información significativa del análisis.
- Usa una muestra representativa: Asegúrate de que la información representen adecuadamente la población o el fenómeno en estudio. Esto evitará conclusiones sesgadas o engañosas.
- Etiquetas claras y descriptivas: Los ejes del diagrama deben tener etiquetas claras que indiquen qué variable se está representando y en qué unidades. Esto facilita la interpretación por parte de cualquier observador.
- Identifica y maneja los datos atípicos: Reconoce y decide cómo tratar los puntos de datos atípicos que pueden distorsionar la representación. A veces, puede ser útil mostrarlos y analizarlos por separado.
- Incluye líneas de tendencia: Agregar una línea de tendencia puede ayudar a visualizar mejor la relación entre las variables.
- Cuida el formato y los colores: Utiliza colores distintos si estás comparando diferentes subconjuntos de datos. Asegúrate de que los puntos de datos sean visualmente accesibles y que el gráfico no esté sobrecargado de información.
- Anotaciones y comentarios: Si hay puntos de interés específicos, como datos atípicos o áreas de mucha concentración de puntos, considera añadir anotaciones que ayuden a interpretarlos.
- Mantén la simplicidad: Evita abrumar el gráfico con demasiadas variables o detalles adicionales que no contribuyan directamente a la comprensión de la relación entre las variables principales.
Siguiendo estos consejos, podrás crear diagramas de dispersión que no solo sean visualmente atractivos, sino también efectivos para analizar y comunicar la relación entre dos variables.
Herramientas para crear un diagrama de dispersión
Existen diversas herramientas que permiten crear diagramas de dispersión de manera sencilla y efectiva. A continuación, se presentan algunas de las más populares:
Microsoft Excel
Excel es una de las herramientas más accesibles y versátiles para crear diagramas de dispersión. Es ampliamente utilizado en ámbitos empresariales, académicos y personales por su facilidad de uso y sus potentes funciones gráficas. Para crear un diagrama de dispersión en Excel, simplemente selecciona los datos y utiliza la función de gráfico de dispersión disponible en la pestaña “Insertar”.
Python
Python es otro lenguaje de programación popular para el análisis de datos, con bibliotecas como matplotlib y seaborn que facilitan la creación de diagramas de dispersión. Al igual que R, proporciona una gran flexibilidad y capacidad para manejar conjuntos de datos grandes y complejos.
Venngage
Venngage es una herramienta en línea que permite crear gráficos y visualizaciones de datos personalizadas, incluidos los diagramas de dispersión. Ofrece una amplia gama de opciones de diseño y plantillas prediseñadas para facilitar la creación de gráficos atractivos y efectivos. Además, permite importar datos directamente desde archivos CSV o Excel para una mayor comodidad.





























